Compound Interest is an extremely important concept in any level of finance. Compound interest can make an enormous difference in the return you get from your investments. As we know, simple interest is the act of earning interest on an investment. If you earned 10% on 100 dollars you would receive 10 dollars every year. On the other hand, with compound interest, that amount grows with interest that you receive. This is true for nearly all investments nowadays, including your bank account!
If you want to see compound interest in action, check out our interactive Compound Interest Calculator, which has charts and graphs that update as you change the saving rules!
An example that is frequently used is the American Indians sale of Manhattan in New York for various items worth about $16. To many that would seem like a very bad deal, since $16 today is not worth much. However, more than 400 years ago, it was a lot of money. If the American Indians had sold the items and invested the money at 8% compounded interest, they would not only have been able to buy back Manhattan today, but would also have a very large leftover of money. This is the real power of compound interest over extended periods of time. You might not have 400 years to save, but even over shorter periods of time, compound interest will add up quickly.
Lets look at an analogy of planting trees that grow and produce other trees that would mimic a ten percent compounded interest. In this example, every tree will grow 10% of a new tree every year.
Year 0: You have saved some money and managed to buy 10 trees and each 10 trees make one tree.
Year 1: The next year you will have 11 trees
Year 2: The year after that 12.1 trees
Year 3: Then 13.3 trees
Year 10: After ten years you will 25.9 trees
If this had been simple interest it would have only been twenty trees.
Visually it looks something like this:
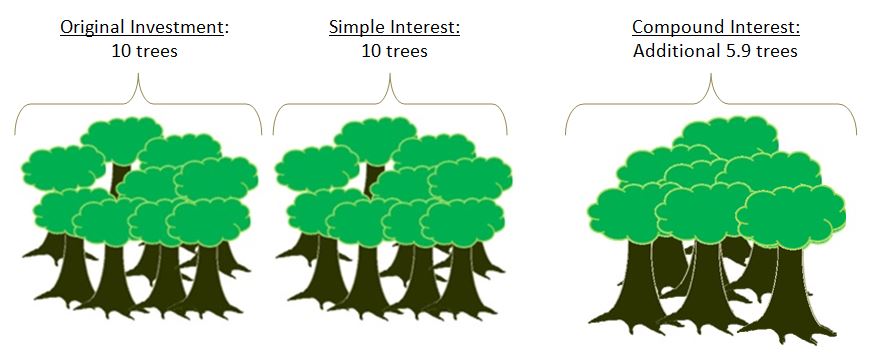
This may not seem like much, but if we look at twenty five years of compound interest versus simple interest, compound interest would get an extra 833 trees!
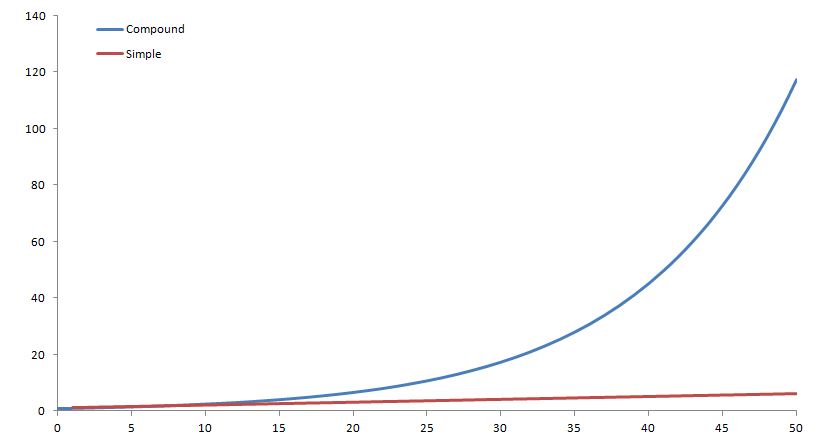
If we look at this graphically, we can see the difference between the two even further.
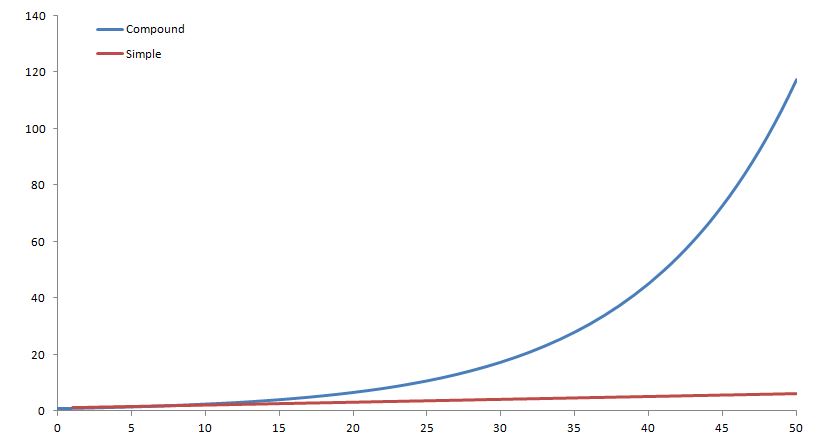
We can see from the graph above that the compound interest curve looks a little like a hockey stick. This will be true for all compound interest curves and is called an exponential curve. From here it is apparent that after 50 years, compound interest makes a very large difference.
Calculation
The calculation of compound interest is quite simple, but can get more complex when we start changing the compounding period. Here, we will look at the basics for compounding once a year and calculating our interest once a year.
A = P(1 + R)t
Example:
If we have a 5% interest and $100 investment:
Year 1: 105=100 (1+0.05)1
Year 2: 110.25=100 (1+0.05)2
Year 2: 115.76=100 (1+0.05)3
or
Year 2: 110.25=105*(1+0.05)
Year 3: 115.76=110.25*(1+0.05)